Energiepotenziale der Kernspaltung
Von der Uran-Aufbereitung bis zur Kernspaltung
Die Erschließung der Energiepotenziale der Kernspaltung begann im zweiten Weltkrieg mit den unmenschlichen Atombomben-Angriffen auf die Zivilbevölkerung von Hiroshima und Nagasaki. Diese von berühmten Physikern mitgetragene Erbsünde wirft einen dauerhaften Schatten auf die Technologiebegeisterung. Die friedliche Nutzung der gewaltigen Potenziale von Kernkraftwerken war auch deshalb immer umstritten. Risiken sind sehr sorgfältig abzuwägen. Es gilt aber ebenso die Unterschiede zwischen früheren Technologien und neuen Entwicklungen zu betrachten.
Inhaltsverzeichnis
- Die Energie der Atomkerne
- Energiepotenziale der Kernspaltung
- Rezeptur der gesteuerten Kernspaltung oder „Der Mann mit der Axt”
- Technologiesuche zur Energiegewinnung mit Kernspaltung in der Generation I
- Leichtwasserreaktoren der Generation II
- Harrisburg — Tschernobyl — Fukushima
- Neue Sicherheitskonzepte und die Generation III
- Kernkraftwerke neu gedacht und die Generation IV
- Die Energie der Sonne durch Kernfusion und aufkommende Technologien
Energiepotenziale der Kernspaltung
Die technologischen Möglichkeiten zur Kernspaltung sind vielfältig. Vor der Betrachtung angewendeter und zusätzlich vorgeschlagener Verfahren erweitern die folgenden Zeilen zuerst die Energiebetrachtungen aus dem Kapitel „Die Energie der Atomkerne“.
Dazu ersetzen wir den ein Kilogramm schweren Goldbarren durch einen ebenso schweren Block aus spaltbarem Uran-235. Diese spezielle Uran-Variante, die Physiker Isotop nennen, besitzt 235 Protonen und Neutronen im Atomkern. Die Anzahl entspricht ungefähr der sogenannten atomaren Masse von Uran. Ein auf den Atomkern auftreffendes Neutron mit der atomaren Masse eins kann den Kern spalten. Nach der Kernspaltung sind die Endprodukte plus die dabei wegfliegenden Neutronen in Abhängigkeit von der Art der Spaltprodukte rund 0,18 atomare Massen leichter als die Ausgangsprodukte. Damit geht also weniger als 0,1 Prozent — ein Tausendstel — der atomaren Masse der Ausgangsprodukte verloren. Die Endprodukte haben somit nach der vollständigen Spaltung von einem Kilogramm Uran ein Gramm der Ursprungsmasse verloren, die in Energie umgewandelt wurde.
Einstein formulierte den Zusammenhang zwischen Energie (E) und Masse (m) über das Quadrat der Lichtgeschwindigkeit © mit der Gleichung E = m ⋅ c2. Diese Gleichung führt zum fast unglaublichen Ergebnis, dass ein Gramm Massenverlust bei der Spaltung aller Atomkerne eines Kilogramms Uran-235 die enorme Energiemenge von 20 Gigawattstunden freisetzt. Diese gewaltige Energiedichte lauert ganz tief innen im Atomkern, der sich zur Größe eines Atoms verhält wie der Stecknadelkopf zu einem Fußballstadion.
Der durchschnittliche Stromverbrauch eines deutschen Haushaltes beträgt 3000 Kilowattstunden (kWh) pro Jahr. Somit reichen 20 Gigawattstunden, das heißt 20 Millionen kWh ein Jahr für ungefähr 7000 Haushalte, eine Stadt mit knapp 20.000 Einwohnern.
Im Kapitel “Die Energie der Atomkerne” lernten wir auch, dass ein Kilogramm schwerer Goldbarren mit dem Energieeinsatz von 0,035 kWh auf einen 10.000 Meter hohen Berg gehoben werden kann. Die weltweit gelagerte Goldmenge beträgt 30 Millionen Kilogramm. Damit reichen 1,05 Millionen kWh, rund eine Gigawattstunde, zum Transport von 30.000 Tonnen Gold auf diesen Berg. Die bei der Spaltung von einem Kilogramm Uran-235 freiwerdende Energiemenge von 20 Gigawattstunden reicht also aus, das Gold der Menschheit zwanzig Mal auf einen zehn Kilometer hohen Berg zu tragen.
Zu erwähnen ist aber, dass diese Berechnung der Energiepotenziale der Kernspaltung eine idealisierte Betrachtung ist. Sie geht davon ausgeht, dass reines Uran-235 eingesetzt und vollständig gespalten wird. Dies entspricht nicht der Realität. Ihre Neugierde auf die verschiedenen Technologien der Kernspaltung wird aber noch gestillt. Vorher kann der mathematisch Interessierte die Berechnung der freiwerdenden Energiemenge im nachfolgenden Exkurs nachvollziehen. Ansonsten überspringen sie diesen Abschnitt einfach. Für das weitere Verständnis ist er nicht erforderlich.
Berechnung der Energiepotenziale der Kernspaltung für Fortgeschrittene
Masse und Anzahl der Atomkerne in einem Kilogramm Uran-235
Die atomare Masseneinheit wird als Einheit der Masse von Atomen benutzt.
Sie ist definiert als ein Zwölftel der Masse eines isolierten Atoms des Kohlenstoff-Isotops mit 12 Nukleonen im Atomkern (Protonen und Neutronen) im Grundzustand.
Auf Basis dieser Definition beträgt die atomare Masseneinheit (u) 1,66⋅10−27 kg.
Annähernd entspricht die Anzahl der Nukleonen (Protonen und Neutronen im Atomkern) der atomaren Masse; z.B. ist die atomare Masse der häufigsten Wasserstoff-Variante rund 1.
Ein Atomkern von Uran-235 besitzt somit mit 235 Nukleonen die atomare Masse von 235 u, also 235⋅1,66⋅10−27 kg gleich 390⋅10-27 kg.
1 kg Uran besteht somit aus 0,00256⋅1027 gleich 2,56⋅1024 Atomkernen.
Massenverlust (Δm; auch Massendefekt genannt) bei der Kernspaltung
Die atomare Masse eines Atomkerns mit 235 Nukleonen plus ein eintreffendes Neutron beträgt 236 u. Nach der Spaltung von Uran unter Freisetzung von drei Neutronen ist die atomare Masse für eine durchschnittliche Zerfallsreaktion beispielsweise 0,18 u kleiner als die atomare Masse der Ausgangsprodukte.
Δm = 0,18 u = (0,18⋅1,66⋅10−27 kg)
Δm = 0,3⋅10−27 kg.
Die Multiplikation mit 2,56⋅1024 Atomkernen in 1 kg Uran ergibt bei vollständiger Spaltung den nachfolgenden Massenverlust.
Δm = 0,3⋅10−27 ⋅ 2,56⋅1024 = 0,77⋅10-03 kg = 0,77 g und somit grob gerundet 1 Gramm
Energiefreisetzung durch Massenverlust pro Atomkern
E = Δm ⋅ c2 (Einstein: Energie gleich Masse mal Quadrat der Lichtgeschwindigkeit)
E = (0,3⋅10−27 kg) ⋅ (3⋅108 m/s)2 = 2,7⋅10−11 Nm
Energiefreisetzung für 1 kg Uran
1 kg Uran besteht aus 2,56⋅1024 Atomkernen.
E = (2,7⋅10−11 Nm / Atomkern) ⋅ (2,56 ⋅ 1024 Atomkerne)
E = 6,9⋅1013 Nm = 6,9⋅1013 Ws rund 20.000.000 kWh = 20.000 MWh = 20 GWh
Produktion von spaltbarem Material
Atomkerne besitzen eine extrem hohe Energiedichte. Nur ein Kilogramm reines Uran-235 kann bei vollständiger Spaltung eine Energiemenge von ungefähr 20 Millionen Kilowattstunden, also 20 Gigawattstunden, freisetzen. Das entspricht ungefähr der durch Verbrennung von rund 3.000 Tonnen Steinkohle gewonnenen Energie. Über die bisher angewendeten technischen Verfahren zum Einsatz von Uran in Kernkraftwerken sprechen wir im nächsten Kapitel.
Da aber der Anteil von reinem Uran-235 in der Natur nur sehr gering ist, benötigen wir noch das Verständnis für Verfahren zur Produktion von technisch nutzbarem Uran.
Natürliches Uran kommt in der Natur vorrangig mit 238 Protonen und Neutronen im Kern vor, nur 0,7 Prozent der Förderung bestehen aus zur Energiegewinnung notwendigem Uran-235. Das gewonnene Uran wird deshalb in Zentrifugen behandelt, um den benötigten Anteil auf ungefähr fünf Prozent zu erhöhen. Dagegen muss für Kernwaffen der Anteil in einem aufwendigen Prozess auf über 90 Prozent erhöht werden. Dieser Unterschied ist auch gut so. Da ein Anreicherungsschritt in Zentrifugen nur einen geringen Trennungsgrad erreicht, muss das Separationsverfahren tausende Male durchlaufen werden. Nur wenige Staaten erreichen den hohen Reinheitsgrad von Uran-235 für kernwaffenfähiges Material. Internationale Abkommen sollen die Weiterverbreitung des Verfahrens verhindern. Dagegen genügt die Anreicherung auf rund fünf Prozent Uran-235 für Kernkraftwerke. Abgereichertes, nicht zur Energiegewinnung nutzbares Uran-238 verbleibt als überflüssiges Uranhexafluorid zur weiteren Lagerung und zum Transport. Die damit verbundenen Gefahren erfordern eine gesonderte Betrachtung (siehe auch Sendung von plusminus zur Urananreicherungsanlage Gronau).
Das angereicherte Urangemisch wird in Brennstäbe eingebracht, die im Kernkraftwerk in den Reaktor eingesetzt und zur Energiegewinnung genutzt werden. Ein Brennelement gilt als ausgebrannt, wenn ungefähr zwei Drittel des zur Spaltung zur Verfügung stehenden Uran-235 verbraucht sind. Bei der Nutzung eines Brennstabes im Kernkraftwerk entsteht aber ein weiteres, höchst gefährliches Material – Plutonium-239. Dieses Isotop bildet ebenso kernwaffenfähiges Material. Ein Kernreaktor herkömmlicher Bauart kann somit nicht kernwaffenfähiges Material nutzen, produziert aber kernwaffenfähige Stoffe.
Energiedichte in Uran-Brennstäben
Produzierte Brennstäbe besitzen in der Praxis einen Anreicherungsgrad von bis zu fünf Prozent. Aufgrund dieses geringen Anteils von Uran-235 in den Brennstäben eines Kernkraftwerkes werden zur Gewinnung von 20 Gigawattstunden Energie statt einem Kilogramm reinen Uran-235 letztendlich zwanzig Kilogramm Uran-Gemisch für die Brennstäbe benötigt. Der Nutzungsgrad der Brennstäbe beträgt rund zwei Drittel. Damit steigt der Brennstoffbedarf auf rund 30 kg Uran-Gemisch im Brennstab pro 20 Gigawattstunden Energiegewinnung durch Kernspaltung.
Schlussendlich wandeln die Generatoren aber nur rund 40 Prozent der gewonnenen Energie nach der Dampferzeugung und dem Antrieb der Turbinen in Strom um. Stromerzeugung im Umfang von 20 GWh benötigt somit rund 75 kg Uran-Gemisch in Brennstäben.
Die zu diesem Wert im Kapital führende grobe Überschlagsrechnung genügt einem Praxisvergleich. Beispielsweise benötigt das schweizerische Kernkraftwerk in Gösgen mit einer Leistung von 1000 Megawatt pro Jahr 20 Tonnen angereichertes Uran. Das Kraftwerk erzeugt dabei rund 8,5 Milliarden Kilowattstunden Strom. Zwanzig Kilogramm des angereicherten Ausgangsstoffes reichen somit zur Gewinnung von 8,5 Millionen Kilowattstunden gleich 8,5 Gigawattstunden elektrischer Energie. Für 20 GWh Strom werden im Kernkraftwerk Gösgen rund 50 Kilogramm angereichertes Uran benötigt.
Um noch einmal zu unserem Beispiel zurückzukehren. Mit dem Einsatz von 50 Kilogramm angereicherten Uran im Kernkraftwerk Gösgen können 30.000 Tonnen Gold zwanzig Mal auf einen 10 Kilometer hohen Berg gebracht werden.
Umwandlung von Elementen bei der Kernspaltung
Um im nächsten Kapital die verschiedenen Technologien zur Kernspaltung vergleichen zu können, benötigen wir noch ein wenig Verständnis für die Abläufe bei der Kernspaltung. Wissenschaftler nutzen zur Erläuterung der Kernspaltung verschiedene Fachbegriffe. Deshalb wenden wir uns zunächst der Klärung dieser Begriffe zu.
Bei verschiedenen schweren Elementen und ihren Varianten, den Isotopen, ist die Kernspaltung grundsätzlich möglich. Um die Spaltung aber technisch effektiv nutzen zu können, wendete sich die Forschung zuerst Uran-235 und Plutonium-239 zu. Das Uran-Isotop besitzt 235 Teilchen im Atomkern mit 92 positiv geladenen Protonen und 143 elektrisch neutralen Neutronen. Im Periodensystem der Elemente besitzt Uran somit die Ordnungszahl 92. Verschiedene Uran-Varianten unterscheiden sich nur in der Anzahl der Neutronen. Im Periodensystem steht Plutonium dem Element Uran am nächsten und besitzt die Ordnungszahl 93. Im Atomkern von Plutonium-239 befinden sich 93 Protonen und 146 Neutronen.
Sogenannte thermische Neutronen können die Kernspaltung auslösen. Der Begriff thermisches Neutron steht für ein langsames Neutron, das sich quasi gemütlich wandernd auf einen Atomkern zubewegt. Das Neutron kann in den Atomkern eindringen, da es als elektrisch neutrales Teilchen nicht von positiv geladenen Protonen abgestoßen wird. Wenn sich das Neutron aber zu schnell bewegt, prallt es vom Atomkern ab. Befindet sich ein thermisches Neutron in der Nähe des Atomkerns, fangen die starken Kernkräfte das Neutron ein und saugen es in den Atomkern. Zur Erläuterung der starken Kernkräfte können Sie zum Kapitel „Fundamente aller Energiequellen“ zurückkehren.
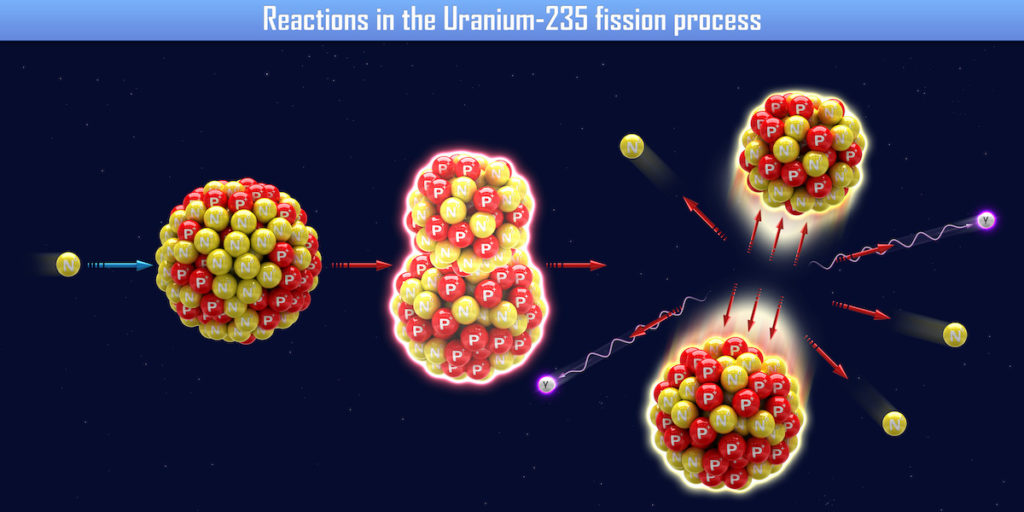
Mit dem Einfang des Neutrons beginnt der Atomkern zu wabern und zerbricht in zwei Teile. Dabei entstehen zwei oder mehrere neue Atome, zum Beispiel Krypton und Barium. Krypton befindet sich im Periodensystem der Elemente bei der Ordnungszahl 36 und Barium bei der Ordnungszahl 56. Es gibt verschiedene mögliche Zerfallsprodukte. Oft beschrieben wird der Zerfall in ein Barium-Isotop mit 139 Teilchen aus 56 Protonen und 83 Neutronen sowie ein Krypton-Isotop mit 94 Teilchen aus 36 Protonen und 58 Neutronen. Aber auch andere Zerfallsprozesse mit unterschiedlicher Protonen- und Neutronenzahl der Spaltprodukte sind möglich. Zusätzlich werden drei Neutronen frei, die mit hoher Geschwindigkeit wegfliegen. Im Gegensatz zu langsamen, thermischen Neutronen nutzen Physiker hier den Begriff schnelle Neutronen.
Energiegewinnung bei der Kernspaltung
Die Berechnung der atomaren Masse der Ausgangsprodukte von Uran–235 plus ein thermisches Neutron sowie der atomaren Masse der Zerfallsprodukte Barium-139, Krypton-94 und der drei schnellen Neutronen ergibt ein interessantes Ergebnis. Die Ausgangsprodukte wiegen 236,05 atomare Masseneinheiten. Dagegen bringen es die Endprodukte nach dem Kernzerfall nur auf 235,840 Masseeinheiten. Die beschriebene Zerfallsreaktion führt also zu einem Verlust von rund 0,21 atomarer Masse. Der Verlust an Masse wird auch als Massendefekt bezeichnet.
Der oben zur Berechnung der gewonnenen Energie genutzte Massenverlust von 0,18 steht für den Mittelwert unterschiedlicher Zerfallsreaktionen. Die bestimmten Größenordnungen reichen aber für unser Ziel, Prozesse bei der Kernspaltung verständlich zu machen sowie die Potenziale der Energiegewinnung abzuschätzen.
Albert Einstein zeigte, dass Energie gleich der Masse mal dem Quadrat der Lichtgeschwindigkeit ist. Hinter diesem kleinen Massenverlust steht also ein hoher Energiegewinn. Die freiwerdende Energie beträgt rund 3⋅10-11 Wattsekunden und somit bei der Spaltung von einem Kilogramm Uran-235, wie schon berechnet, 20 Gigawattstunden. Dies entspricht dem Einsatz von rund 2.500 Tonnen Steinkohle im Kohlekraftwerk.
Die wegfliegenden schnellen Neutronen können keine neuen Kernspaltungen auslösen. Aufgrund ihrer hohen Geschwindigkeit prallen sie am Atomkern einfach ab. Um eine Kettenreaktion weiterer Kernspaltungen auszulösen, müssen diese Neutronen abgebremst werden. Kernenergetiker sprechen bezüglich der Abbremsung von der Moderation. Verschiedene Mittel sind geeignet, um Neutronen zu moderieren. Zum Beispiel besitzt Wasser die notwendigen Eigenschaften. Wassermoleküle bestehen mit zwei Wasserstoffatomen und einem Sauerstoffatom aus leichten Teilchen. Neutronen können somit beim Zusammenstoß ihre Bewegungsenergie gut abgeben, ähnlich dem Stoß zwischen zwei Billardkugeln.
Zum Start der Kettenreaktion wird eine Neutronenquelle benötigt. Wenn der Prozess läuft, können freiwerdende und verlangsamte Neutronen weitere Spaltungen in einer Kettenreaktion auslösen. Da aber ein Neutron mit der Kernspaltung drei Neutronen erzeugt, steigt die Zahl der Spaltungen exponentiell. Ohne Steuerung, das heißt ohne Verringerung der freigesetzten Neutronen würde die vorhandene Menge an Uran–235 in einer gewaltigen Explosion schlagartig vollständig gespalten. Diese gewaltige Kraft der Atombombe wurde zuerst in Hiroshima und Nagasaki freigesetzt.
Eine Kernspaltung darf nur genau eine weitere Spaltung auslösen, um die Kettenreaktion zu verhindern. Dazu wird dem Wasser Borsäure beigefügt oder es werden in den Kernreaktor Regelstäbe aus Bor und dem Metall Kadmium eingebracht. Diese Materialart kann Neutronen einfangen, ohne selbst zu reagieren. Durch die Steuerung der Regelstäbe kann die Anzahl der Kernspaltungen verändert werden. Damit lässt sich die Leistung des Reaktors steuern, das heißt die Reaktivität des Reaktors steigern oder verringern.
Betriebspausen und Abfälle
Um die Unterschiede zwischen verschiedenen Technologien zur Kernspaltung zu beleuchten, benötigen wir noch eine kurze Betrachtung der Betriebspausen eines Kernreaktors, der Erneuerung von Brennmaterialien sowie der entstehenden Abfälle.
Bei herkömmlichen Kernreaktoren mit Uran als Festbrennstoff in stabförmigen Elementen verbleibt die Energiequelle auch in Betriebspausen in gleichbleibender Konzentration im Reaktor. Es erfolgen also weiterhin Kernspaltungen innerhalb der Brennstäbe, womit dauerhaft Wärme produziert wird. Dies erfordert eine ständige Kühlung auch während der Betriebspausen. Wenn im Störungsfall die Kühlung ausfällt, kann somit das Brennmaterial im Reaktor auch im eingestellten Betrieb überhitzen. Die Kernschmelze droht. Im Rahmen dieses Prozesses wird ab bestimmten Temperaturen Wasser in Wasserstoff und Sauerstoff aufgespalten. Somit besteht die Möglichkeit der Zerstörung des Reaktors durch eine Knallgasreaktion, wie es im Kernkraftwerk Fukushima der Fall war.
Die analoge Betrachtung gilt für sogenannte, ausgebrannte Brennstäbe. Sie werden aus dem Kernreaktor entfernt und durch neue Brennstäbe ersetzt. Die ausgebrannten Brennstäbe enthalten aber weiterhin rund ein Drittel ihres ursprünglichen Gehaltes an Uran-235. Somit erfolgen in den Brennstäben weiterhin Kernspaltungen. Die noch hoch radioaktiven Elemente müssen über Jahre gekühlt werden. Dies erfolgt in Abklingbecken außerhalb des Sicherheitsbehälters des Reaktors unter dem normalen Dach eines Reaktorgebäudes. Die weitere Aktivität der Uranstäbe im Zusammenhang mit dem möglichen Ausfall der Kühlung birgt somit ebenso die Gefahr der Überhitzung, des Schmelzens von Brennelementen sowie des Eindringens in den Erdboden.
Schlussendlich muss der ausgebrannte Brennstoff nach dem Abkühlen in sogenannten Castor-Behältern der Zwischenlagerung zugeführt werden. Diese Behälter schützen vor dem Austreten der radioaktiven Strahlung. Derartig in Zwischenlagern aufbewahrt, wartet der hoch radioaktive Müll auf das bisher ungeklärte Verfahren zur Endlagerung. 300.000 Tonnen dieses Mülls pro Jahr fallen weltweit an und müssen der Endlagerung zugeführt werden. Die Halbwertszeit der Reststoffe ist so hoch, dass teilweise zehntausende Jahre vergehen müssen, ehe die Strahlung auf die Hälfte des Ursprungswertes abnimmt. Deshalb sind geologische Schichten zu finden, in denen das Material für hunderttausende Jahre sicher eingeschlossen bleibt. Aufgrund dieser fast unlösbaren Aufgabe konnten bisher in Mitteleuropa noch keine geeigneten Endlager ausgewählt werden.
Diese kurze, populärwissenschaftliche Einführung in die Förderung, Aufbereitung und Nutzung von Uran sowie die Lagerung des radioaktiven Mülls verwenden wir, um in den nächsten Kapiteln Technologien zur Energiegewinnung durch Kernspaltung zu vergleichen und damit die Energiepotenziale der Kernspaltung zu erschließen.
“Energiepotenziale der Kernspaltung” — Leimen / Heidelberg — 1. November 2022
Andreas Kießling, energy design