Quantenmechanik — Versuch einer Einführung in eine schwer begreifbare Welt |
| Die Quantenmechanik verständlich zu erläutern, kann als 80 Jahre anhaltender Versuch bezeichnet werden. Lange verstanden selbst Physiker nicht, was Planck mit seinem Postulat der diskreten Energiezustände nach Untersuchung der Strahlung des schwarzen Körpers im Jahre 1900, Einstein mit seinem photoelektrischen Effekt im Jahre 1905, wofür er übrigens 1921 den Nobelpreis erhielt, Nils Bohr mit der Untersuchung der Atomstruktur im Jahre 1921 (Nobelpreis 1922), de Broglie mit seinem Vorschlag der Materiewellen im Jahre 1921, Untersuchungen wie das Doppelspaltexperiment und der Stern-Gerlach-Versuch, sowie letztendlich die Entwicklung der Quantentheorie durch Erwin Schrödinger (Nobelpreis 1933), Paul Dirac (Nobelpreis 1932) und Wolfgang Pauli (Nobelpreis 1945) seit der Aufstellung der Schrödingergleichung im Jahre 1926 anrichteten.
Letztendlich startet seit den 80er Jahren des 20. Jahrhunderts eine unbekümmerte Physikergeneration die Anwendung der Quantentheorie mit Nanotechnologie, künstlichen Quantensystemen, Quantencomputern, Quanteninformatik, Quantenkrypthografie und Teleportation verschränkter Teilchen, die Vision des Beamens aus der Startrekreihe „Raumschiff Enterprise“ vor den Augen, obwohl immer noch viele grundsätzliche Probleme der Quantenmechanik ungelöst sind und so manche Physiker mit Richard Feynman (Nobelpreis 1965) übereinstimmen, der sagte: „Ich denke, ich kann sagen, dass niemand die Quantenmechanik verstanden hat.“ Exotisch war von Anfang an die Erkenntnis, dass Materie in Teilchen- und Wellenform existiert und die Wahrnehmung davon abhängt, wie wir eine Messung organisieren. Im Doppelspaltexperiment ist die Materie eine Welle, wenn beide Spalte offen sind, und wir sehen Interferenz. Schließen wir jedoch einen Spalt, wird die Materie zum Teilchen, denn wir versuchen einen Zustand zu messen. Wir versuchen den Ort zu bestimmen und verlieren damit die Information über den Impuls und damit die Energie. Sind wir mit der Messung des Impulses zufrieden, verlieren wir die Information über den Ort. Dies drückte Heisenberg mit der Unbestimmtheitsrelation aus. Insbesondere können sich immer noch viele Physiker nicht damit abfinden, dass wir eine rein subjektive Welt haben sollen, deren Zustand vom Messprozess abhängt. Mit der Quantenmechanik beschreiben wir die Welt durch eine Funktion, in der nur die Wahrscheinlichkeiten aller möglichen Zustände stecken. Dabei existieren alle möglichen Zustände parallel und erst die Messung manifestiert einen Zustand in der Realität. Selbst bei Messungen, bei denen wir nicht hinschauen, manifestiert sich ein Zustand aller möglichen Zustände. Die Natur lässt sich nicht überlisten. Schrödingers Katze, die gleichzeitig lebt und tot ist, wurde dafür zum Sinnbild. Diese Abhängigkeit der Realität vom Messprozess stammt aus der Kopenhagener Deutung von Bohr und Heisenberg. Damit konnte sich selbst Einstein nicht abfinden und heute gibt es wieder Entwicklungen, die die Natur auf eine objektive Grundlage stellen wollen. Andere halten sich von diesem Streit fern und nutzen die Quantentheorie für exotische technische Entwicklungen. Am Beginn der Aneignung der Quantentheorie stehen viele Vereinfachungen, um ein grundlegendes Verständnis zu erreichen. Wir geben uns mit der Quantenmechanik zufrieden und hierbei mit nichtrelativistischen Geschwindigkeiten, das heißt Geschwindigkeiten weit unter der Lichtgeschwindigkeit. Außerdem betrachten wir nur skalare Felder, wie zum Beispiel die Gravitationskraft oder das elektrostatische Feld und lassen hohe Geschwindigkeiten oder den Magnetismus beiseite. Auf vielen dieser Vereinfachungen beruht letztendlich auch die Schrödingergleichung. Mit weiteren Komplikationen zum Beispiel im relativistischen Bereich beschäftigte sich dann unter anderem Dirac. Um den Elektromagnetismus einzubeziehen und die Atomstrahlung zu verstehen, waren weitere Arbeiten zur Quantenelektrodynamik bis hin zu Richard Feynman, Schwinger und Tominaga notwendig. Bleiben wir aber bei der Schrödingergleichung. Denn sie lieferte erstaunliche Übereinstimmungen mit der Natur, insbesondere bei der Vorhersage der Atomstruktur in Form des Schalenmodells, der Orbitale und der Energieniveauaufspaltungen in der Hyperfeinstruktur, was letztendlich auch die Grundlage heutiger bildgebender Verfahren wie der Magnetischen Resonanztomografie (MRT) ist. Wie ist die Schrödingergleichung also zu verstehen, ohne gleich auf den komplizierten mathematischen Apparat zu sprechen zu kommen? Wie wechselt nun das System seinen Zustand? Ein Gerät wirkt auf das System ein und verändert seinen Zustand. Dieses Gerät (zum Beispiel externes Feld oder Messgerät) nennen wir Operator, das auf einen Zustand Ψ wirkt und einen neuen Zustand erzeugt. Nichts anderes sagt die Schrödinger-Gleichung aus. Der sogenannte Hamilton-Operator H wirkt auf die Wellenfunktion Ψ (beschreibt den Systemzustand als Amplituden an allen Orten r zu einer bestimmten Zeit t) und bewirkt damit eine Veränderung der Wellenfunktion in der Zeit t (d/dt), das heißt
Interessant ist die Frage, ob es Zustände Ψ (Vektoren im Hilbertraum) gibt, die nach der Transformation durch den Hamiltonoperator unverändert bleiben und sich damit zeitlich nicht verändern. Diese Fragestellung nennt sich Eigenwertaufgabe, das heißt H Ψ(r) = λ Ψ(r). Mit Hilfe der Einheitsmatrix I können wir die Gleichung auch in folgender Form schreiben: |
| (H — λ E ) Ψ(r) = 0 |
| Gesucht werden die Eigenvektoren Ψ(r) und zugehörige komplexe Vielfache λ, die diese Gleichung erfüllen. Da wir beliebig viele Dimensionen des Zustandes Ψ haben können, lösen wir hier also n‑dimensionale Gleichungssysteme mit n Unbekannten. Aus der Mathematik wissen wir, genauer aus der linearen Algebra und der Matrizenrechnung, dass wir nichttriviale Lösungen erhalten, wenn die Determinante dieser Matrix gleich Null ist. Nichtmathematiker sollen hier nicht gelangweilt werden und springen über den nächsten, kursiv gedruckten Abschnitt, der nur kurz den Lösungsweg benennt.
Die Gleichung heißt charakteristische Gleichung der Matrix H und ihre Auflösung führt zu einem Polynom n‑ten Grades bezüglich λ: p(λ) = det(H — λ E), dem sogenannten charakteristischen Polynom von H. In der Quantenmechanik sind diese Vielfache λ die Eigenwerte E, die die Energiezustände beschreiben, auf denen sich die Teilchen im stationären Zustand befinden können. Man erhält für ein Teilchen, das sich in einem sogenannten Potentialtopf befindet (beispielsweise Elektron auf der Bahn um einen Wasserstoffkern) und sich damit nicht frei bewegen kann, diskrete Energiezustände. Es kann also nicht jeden beliebigen Energiezustand einnehmen. Bei Übergängen zwischen zwei Energiezuständen werden Energiequanten benötigt oder frei. Am Schluss sei noch einmal kurz zusammengefasst. Wir haben hier den Zustand von Teilchen über ihren Ort und Impuls quantenmechanisch beschrieben. Diese Betrachtungsform gilt natürlich auch für andere Zustandsformen, die Polarisationsrichtung von Licht in der Quantenoptik oder den Spin von Elektronen (rechts- oder linksdrehend) als mögliche Beschreibungsform eines Zustandes in der Quanteninformatik. Die Anzahl der ein System vollständig beschreibenden Merkmale bestimmt die Anzahl der Dimensionen des Zustandes. Alle möglichen Zustände des Systems in diesem n‑dimensionalen Raum beschreiben den Hilbertraum. Auf diesen Zustand wirkt ein anderes System (Operator) ein und überführt diesen Zustand in einen anderen Zustand, das heißt das System bewegt sich im Hilbertraum. Dazu hat Dirac eine einfache Schreibweise in folgender Form eingeführt, bei der ein Operator H auf einen Zustandsvektor Ψ einwirkt und damit einen neuen Zustand Φ erzeugt. |Φ> = H |Ψ> Wir betrachten mit der Wellenfunktion Ψ also die Amplituden von Zuständen, mit dem Quadrat dieser Amplituden, die Wahrscheinlichkeit für den Aufenthalt in verschiedenen Zuständen, sowie mit einwirkenden Operatoren Zustandsveränderungen (Bewegungen im Hilbertraum), wobei bei stationären Lösungen der Zustand auch erhalten bleiben kann. |
Januar 2005, copyright by Andreas Kießling
Die Postulate der Quantenmechanik
Die Quantenmenchanik ist ein physikalischer Apparat zur Entwicklung physikalischer Theorien. Damit erzählt uns die Quantenmechanik nicht selbst, welchen Gesetzen ein physikalisches System unterliegt, sondern sie führt ein konzeptionelles und mathematisches Set zur Entwicklung solcher Gesetze ein. Die folgenden Postulate der Quantenmechanik führen zu einer Verbindung der physikalischen Welt und dem mathematischen Formalismus der Quantenmechanik.
Postulat 1Zugehörig zu einem jeden physikalischen System ist ein komplexer Vektorraum (der Hilbertraum), bekannt als der Zustandsraum des Systems. Das System ist komplett durch seinen Zustandsvektor beschrieben, welcher ein Einheitsvektor im Zustandsraum des Systems ist. Postulat 2Die Evolution eines geschlossenen Quantensystems wird durch eine unitäre Transformation beschrieben. Das heißt, der Zustand Postulat 3Quantenmessungen werden durch eine Sammlung von Messoperatoren beschrieben. Dies sind auf den Zustandsraum des zu messenden Systems wirkende Operatoren. Der Index m bezieht sich auf das Messergebnis, das in dem Experiment vorkommen kann. Wenn der Zustand des Quantensystems vor der Messung Postulat 4Der Zustandsraum eines zusammengesetzten Systems ist das Tensorprodukt der Zustandsräume der physikalischen Systemkomponenten. Postulat 1 stellt die Arena für die Quantenmechanik dar, indem es spezifiziert, wie der Zustand eines isolierten Quantensystems beschrieben werden kann. Postulat 2 erzählt uns, dass die Dynamik eines geschlossenen Quantensystems durch die Schrödingergleichung beschrieben wird, und damit durch eine unitäre Transformation. Postulat 3 erzählt uns mit der Vorschrift für die Beschreibung einer Messung, wie Information aus unserem Quantensystem extrahiert werden kann. Postulat 4 wiederum gibt uns mit der Beschreibung zusammengesetzter Systeme eine Anleitung, wie Zuständsräume verschiedener Quantensysteme kombiniert werden können. |
| Quantum Computation and Quantum Information, Michael A. Nielsen and Isaak L. Chuang, Cambridge University Press, 2000 |

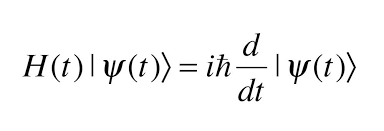 Da man in der Quantenmechanik mit imaginären Zahlen arbeitet, um Phase sowie Amplitude der Welle gleichzeitig zu beschreiben, steht die imaginäre Größe i in der Formel, die mit dem Heisenbergschen Wirkungsquantum h multipliziert wird. Das Wirkungsquantum kommt hier als kleinstmöglicher Vervielfacher ins Spiel, da das Produkt der Messgenauigkeit des Ortes und der Messgenauigkeit des Impulses eines Teilchens nie kleiner als das Wirkungsquantum sein kann (Heisenbergsche Unschärferelation). Misst man den Aufenthaltsort eines Teilchens sehr genau, wird die Impulsmessung ungenau und umgekehrt.
Da man in der Quantenmechanik mit imaginären Zahlen arbeitet, um Phase sowie Amplitude der Welle gleichzeitig zu beschreiben, steht die imaginäre Größe i in der Formel, die mit dem Heisenbergschen Wirkungsquantum h multipliziert wird. Das Wirkungsquantum kommt hier als kleinstmöglicher Vervielfacher ins Spiel, da das Produkt der Messgenauigkeit des Ortes und der Messgenauigkeit des Impulses eines Teilchens nie kleiner als das Wirkungsquantum sein kann (Heisenbergsche Unschärferelation). Misst man den Aufenthaltsort eines Teilchens sehr genau, wird die Impulsmessung ungenau und umgekehrt.